
Wyniki badań
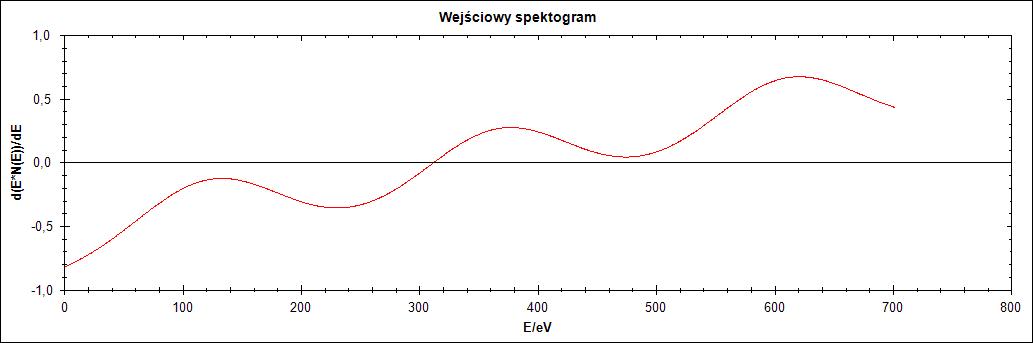
Przedstawione poniżej wyniki poukładane są według rodzaju wykresu wejściowego. Przedstawiono spektrogram oryginalny, zaszumiony oraz wygładzony. Następnie dla każdego z nich przedstawiono wyniki działania algorytmu dla czterech wartości parametru Δ.
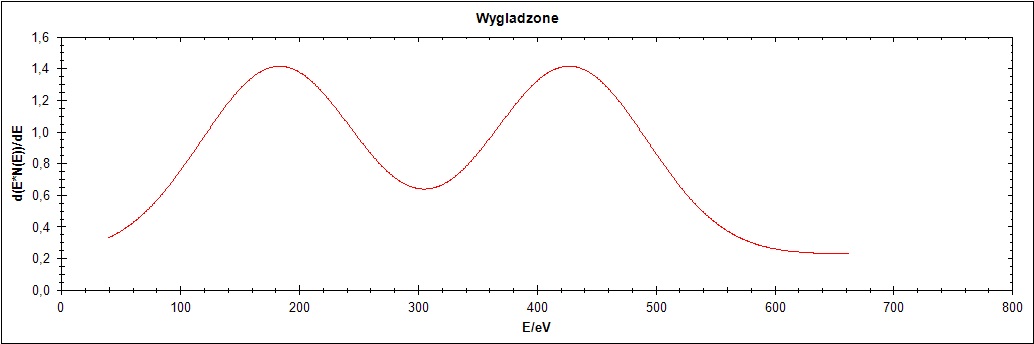
Pierwszy przebieg charakteryzuje się „ostrzem” pomiędzy łączeniem dwóch przebiegów Gaussa. Jak widać na Rysunku 1 po zaszumieniu i wygładzeniu szpilka ta zanika, ponieważ wygładzanie polega na dopasowaniu funkcji wielomianowej drugiego stopnia.
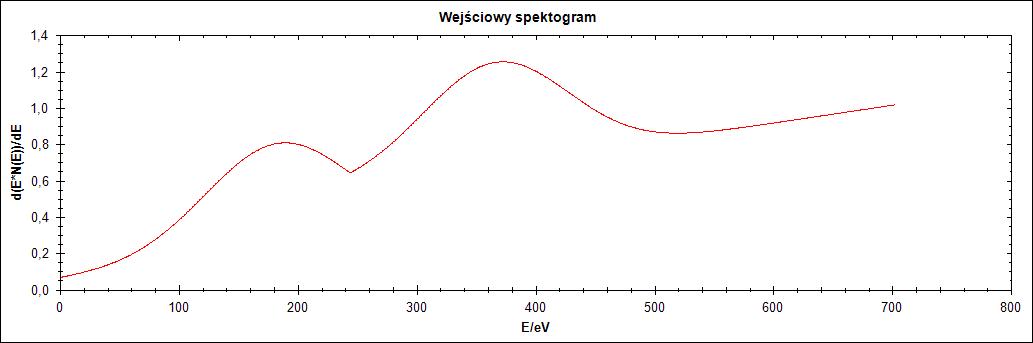
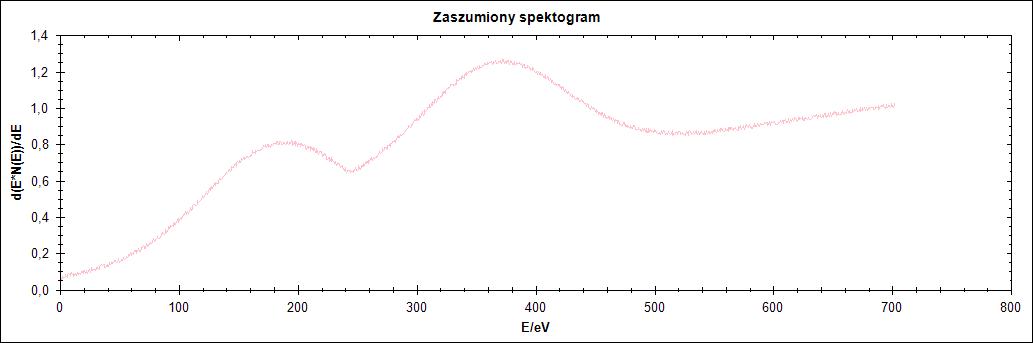
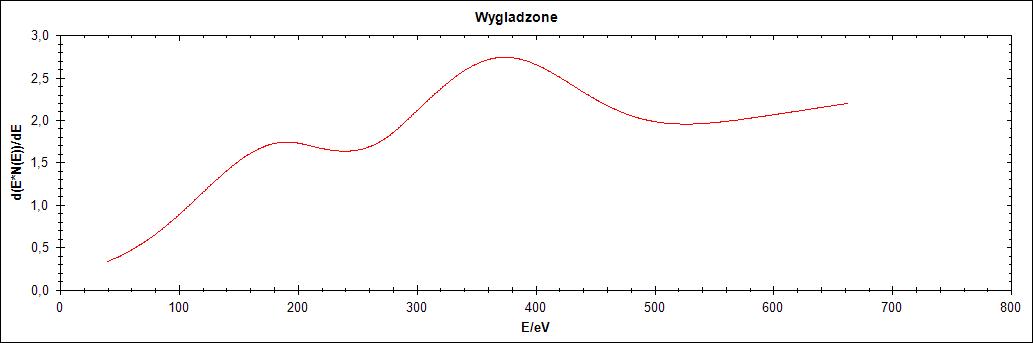
Rysunek 1. Przebieg 1) i jego warianty: zaszumiony oraz wygładzony
Na Rysunkach 2-4 widać wyniki działania algorytmu na kolejnych przebiegach z Rysunku 1 dla kolejnych wartości parametrów Δ.
Δ = 1
Δ = 2
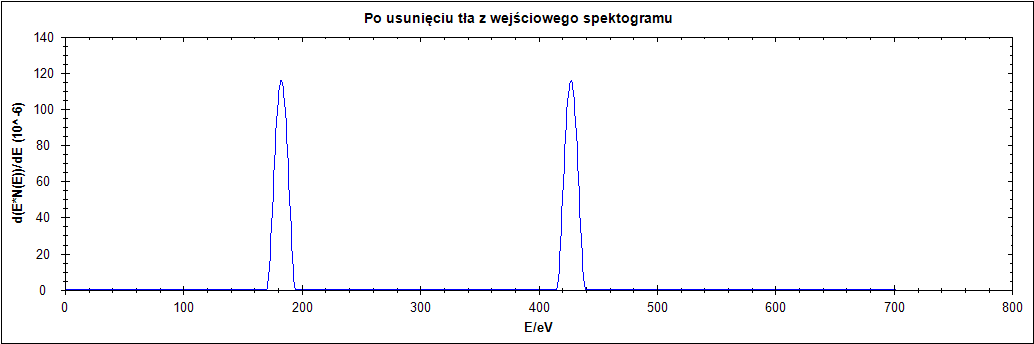
Δ = 25
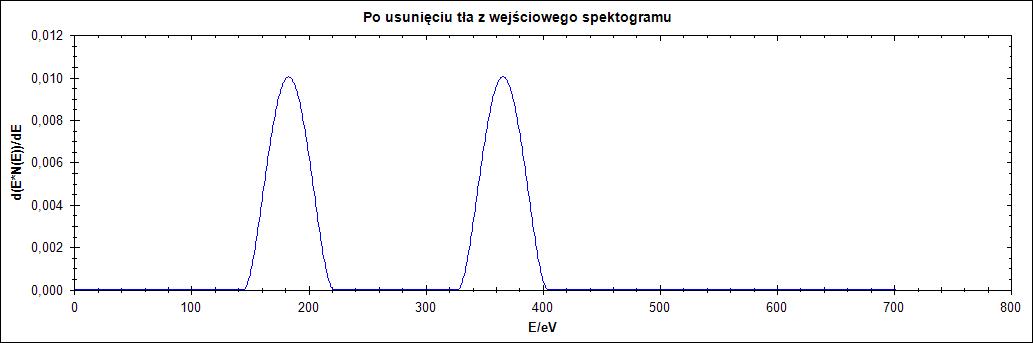
Δ = 77
Rysunek 2. Działanie algorytmu dla przebiegu oryginalnego dla parametru Δ = 1,2,25,77 w kolejności od góry do dołu
Na rysunku 2. wyraźnie widać wpływ parametru delta. Dla zbyt małych jego wartości przebieg zostaje wyzerowany natomiast przy jego zwiększaniu następuje przesunięcie przebiegu oraz zwiększenie szerokości połówkowej piku.
Δ = 1
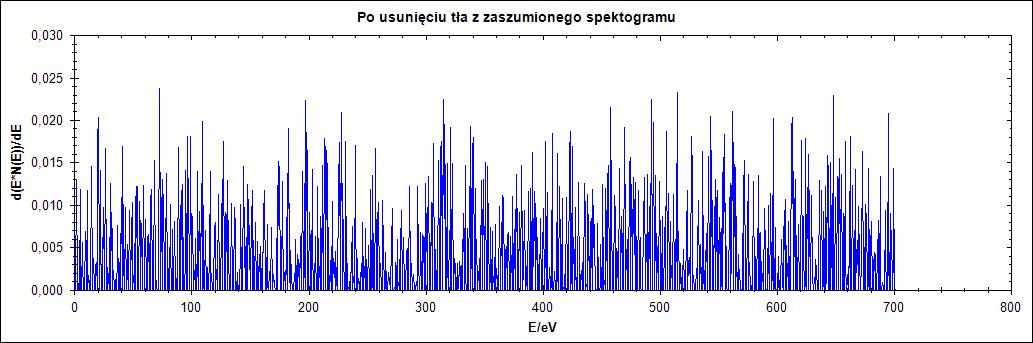
Δ = 2
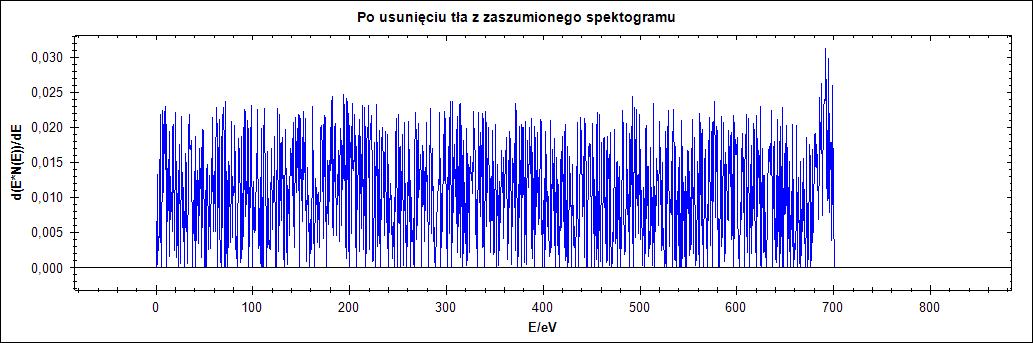
Δ = 25
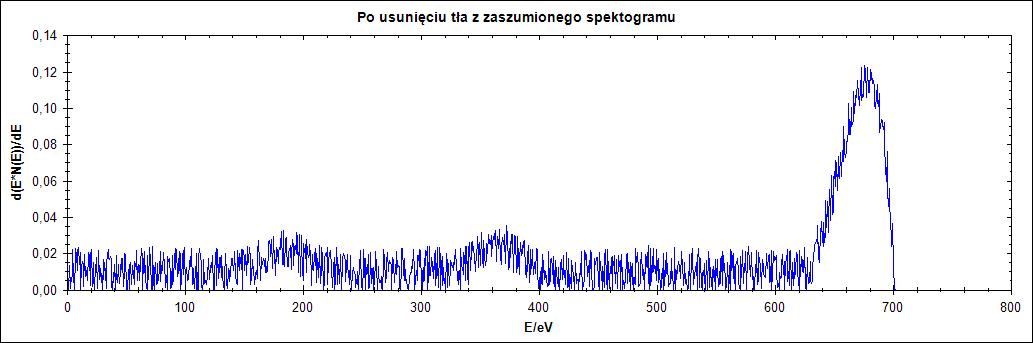
Δ = 77
Rysunek 3. Działanie algorytmu dla przebiegu zaszumionego dla parametru Δ = 1,2,25,77 w kolejności od góry do dołu
Na rysunku 3. widać, że mocno zaszumiony przebieg wręcz uniemożliwia odczytanie pików. Dla parametru delta równego 77 widzimy mocne przesunięcie przebiegu.
Δ = 1
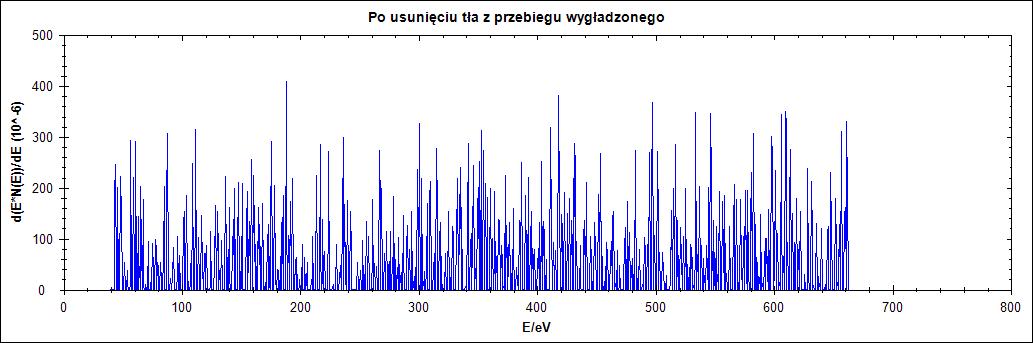
Δ = 2
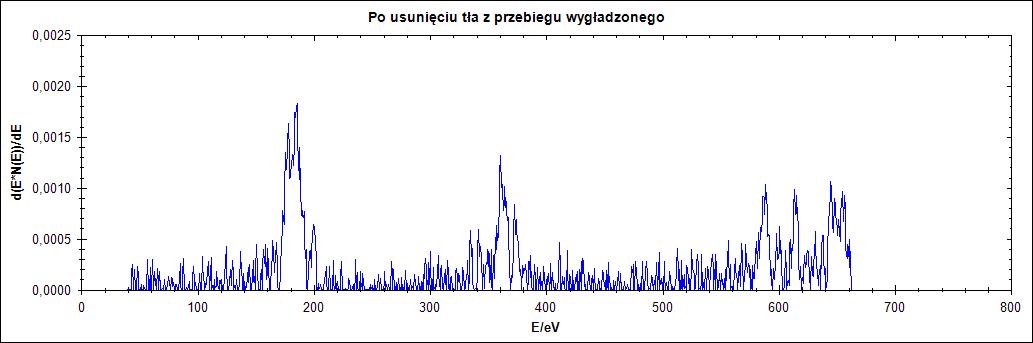
Δ = 25
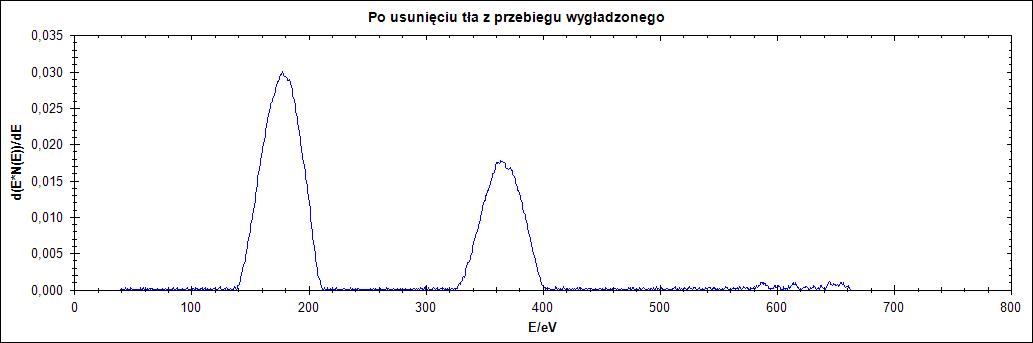
Δ = 77
Rysunek 4. Działanie algorytmu dla przebiegu wygładzonego dla parametru Δ = 1,2,25,77 w kolejności od góry do dołu
Na rysunku 4. widzimy, że jeśli przebieg wejściowy zostanie poddany wygładzaniu algorytmem Savitzky’ego – Golay’a otrzymamy znacznie lepsze wyniki. Dla niskich wartości parametru delta nadal nie otrzymujemy nic sensownego to jednak dla wartości 25 i szczególnie 77 otrzymujemy sensownie usunięte tło.
Drugi przebieg jest najbardziej typowym wykresem, z którego można zaobserwować standardowe działanie algorytmu. Rysunek 5 przedstawia wszystkie warianty tego przebiegu.
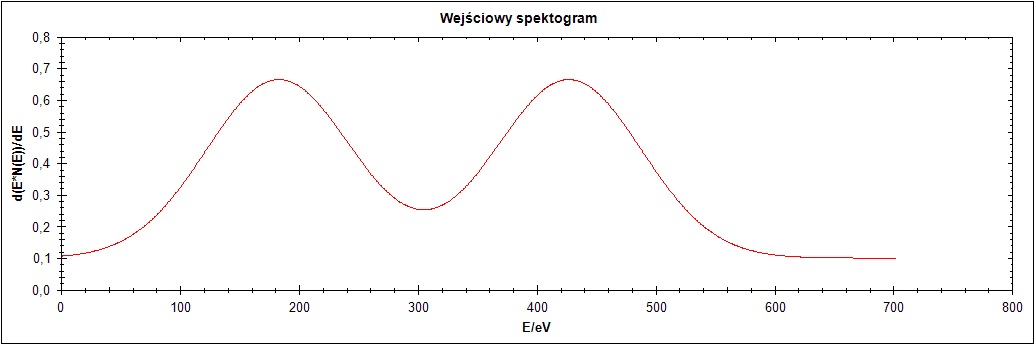

Rysunek 5. Przebieg 2) i jego warianty: zaszumiony oraz wygładzony
Na Rysunkach 6-8 widać wyniki działania algorytmu na kolejnych przebiegach z Rysunku 5 dla kolejnych wartości parametrów Δ.

Δ = 1
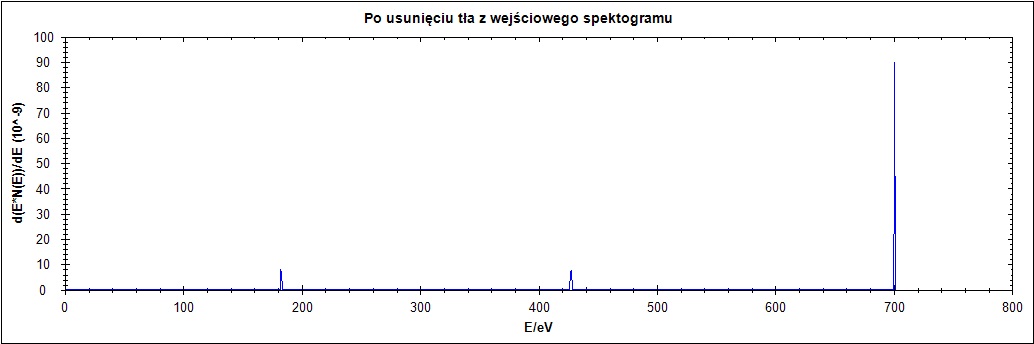
Δ = 2
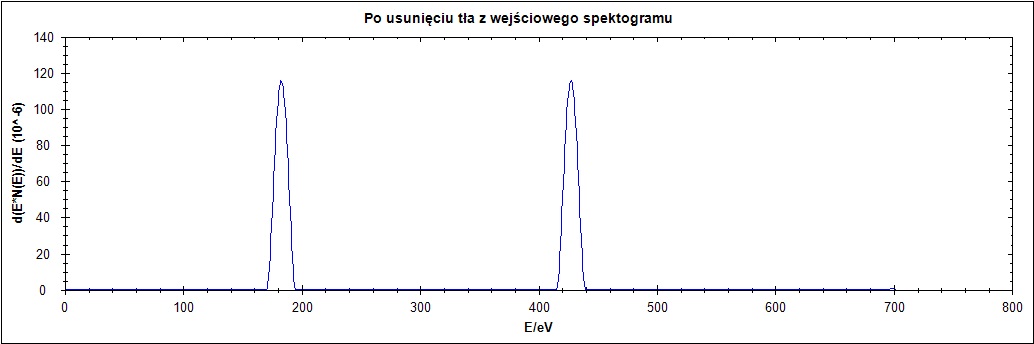
Δ = 25
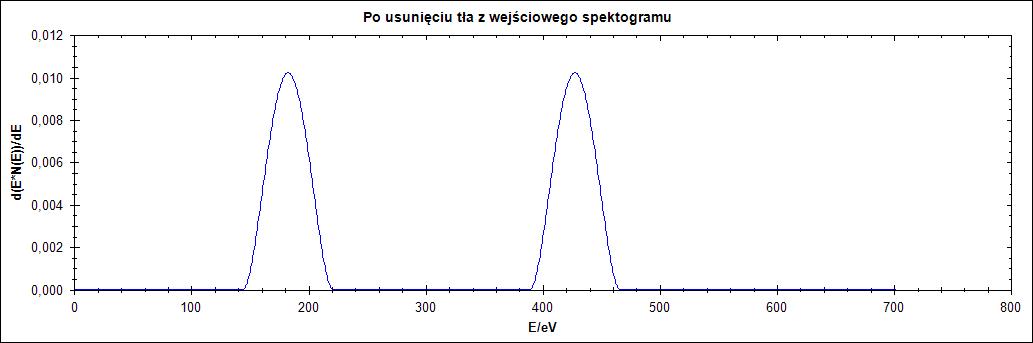
Δ = 77
Rysunek 6. Działanie algorytmu dla przebiegu oryginalnego dla parametru Δ = 1,2,25,77 w kolejności od góry do dołu
Na rysunku 6. wyraźnie widać wpływ parametru delta. Dla zbyt małych jego wartości przebieg zostaje wyzerowany, a dla wartości równej 2 na końcu przebiegu pojawia się szpilka. Przy zwiększaniu wartości delta następuje przesunięcie przebiegu oraz zwiększenie szerokości połówkowej piku.
Δ = 1
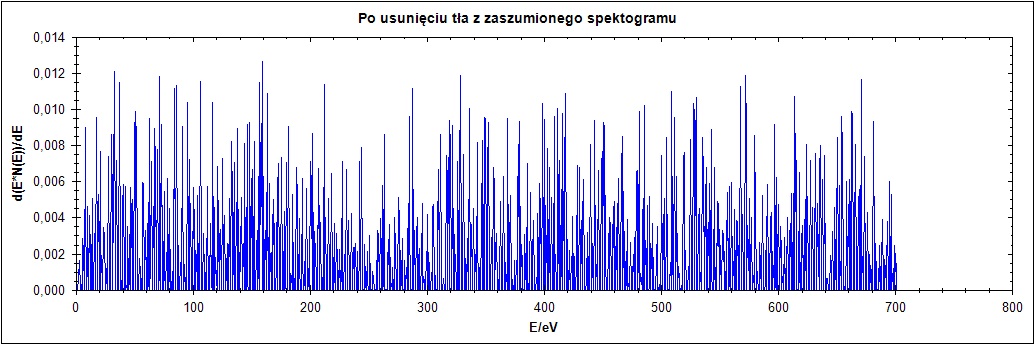
Δ = 2
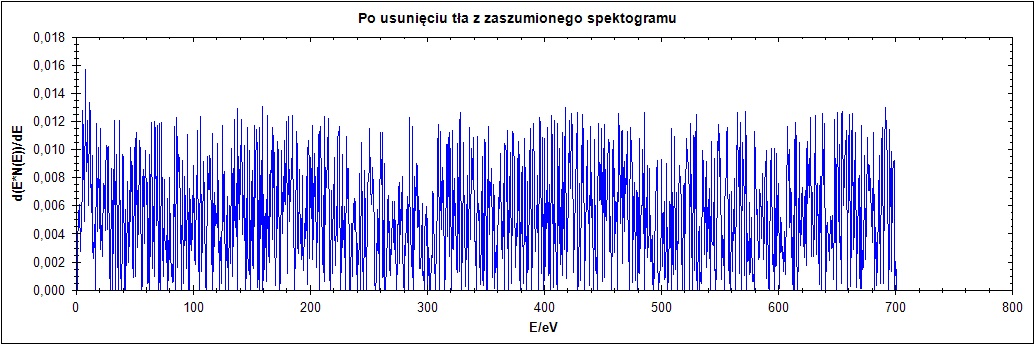
Δ = 25
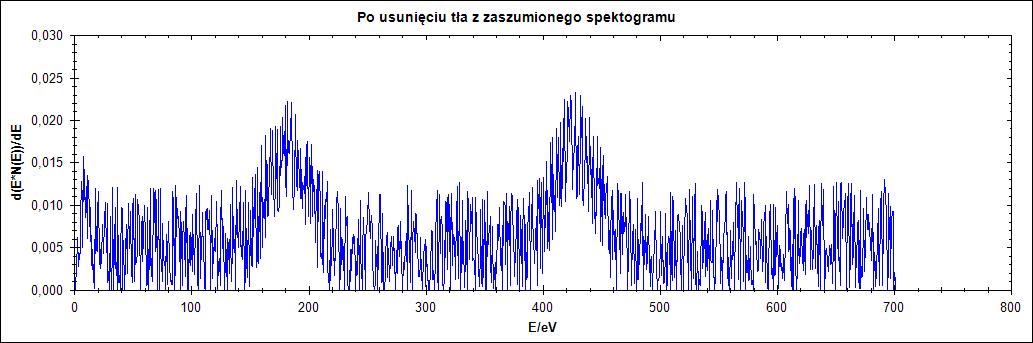
Δ = 77
Rysunek 7. Działanie algorytmu dla przebiegu zaszumionego dla parametru Δ = 1,2,25,77 w kolejności od góry do dołu
Na rysunku 7. widać, że mocno zaszumiony przebieg wręcz uniemożliwia odczytanie pików. Dla parametru delta równego 77 istnieje jednak możliwość odczytania wartości piku.

Δ = 1
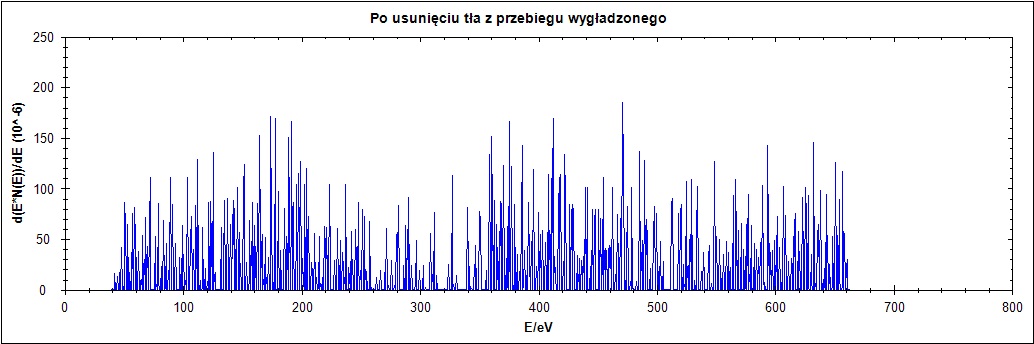
Δ = 2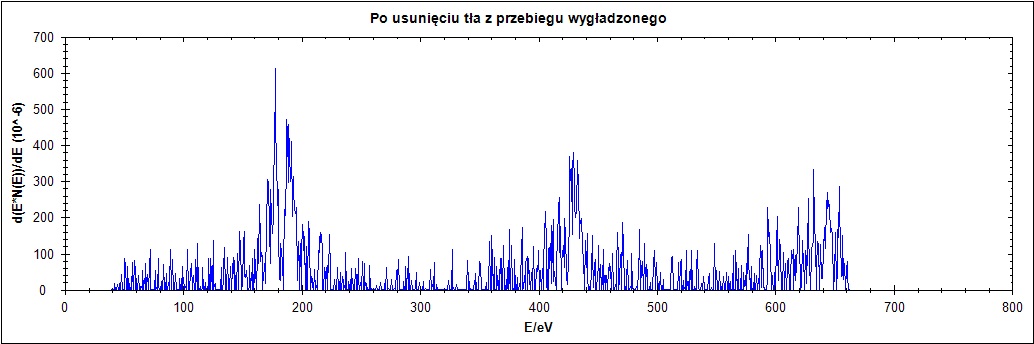
Δ = 25
Δ = 77
Rysunek 8. Działanie algorytmu dla przebiegu wygładzonego dla parametru Δ = 1,2,25,77 w kolejności od góry do dołu
Na rysunku 8. widzimy, że jeśli przebieg wejściowy zostanie poddany wygładzaniu algorytmem Savitzky’ego – Golay’a otrzymamy znacznie lepsze wyniki. Dla niskich wartości parametru delta nadal nie otrzymujemy nic sensownego to jednak dla wartości 25 i szczególnie 77 otrzymujemy sensownie usunięte tło.
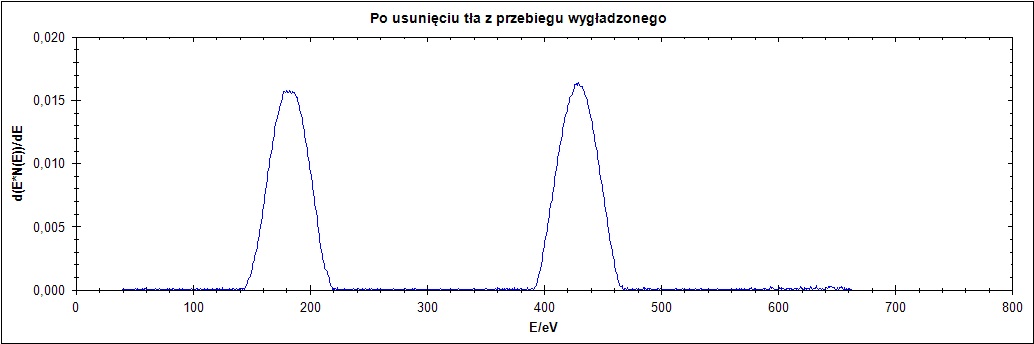
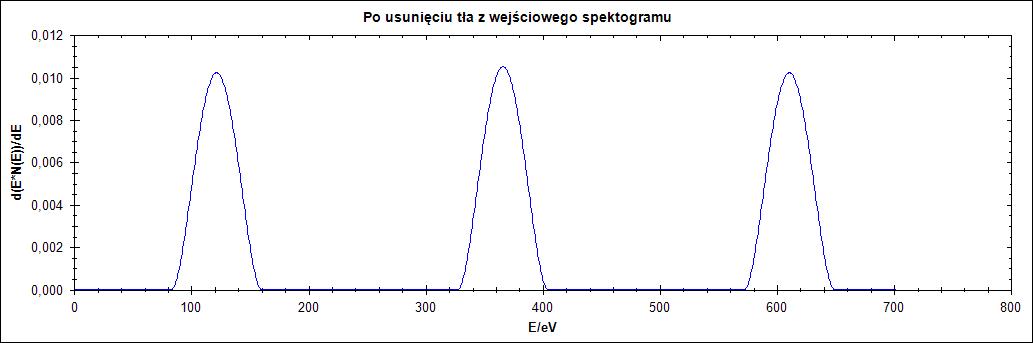
Trzeci przebieg ma mniejsze różnice między maksimami, charakteryzuje się tym że przechodzi przez oś OX. Na Rysunku 9 przedstawiono wszystkie warianty tego przebiegu użyte w badaniu algorytmu.
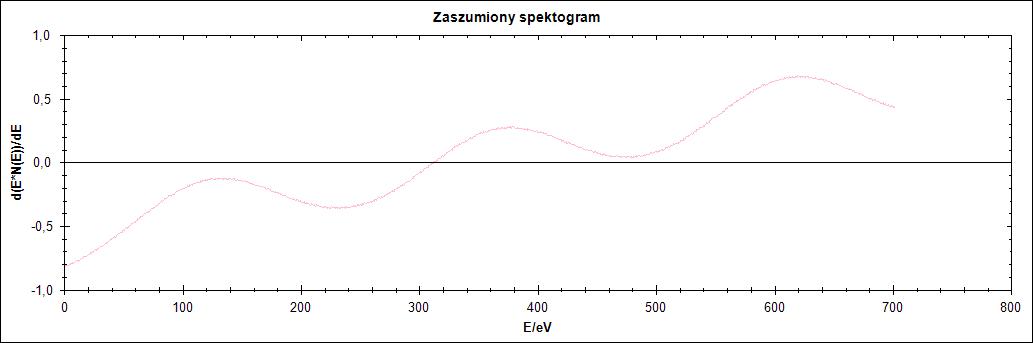
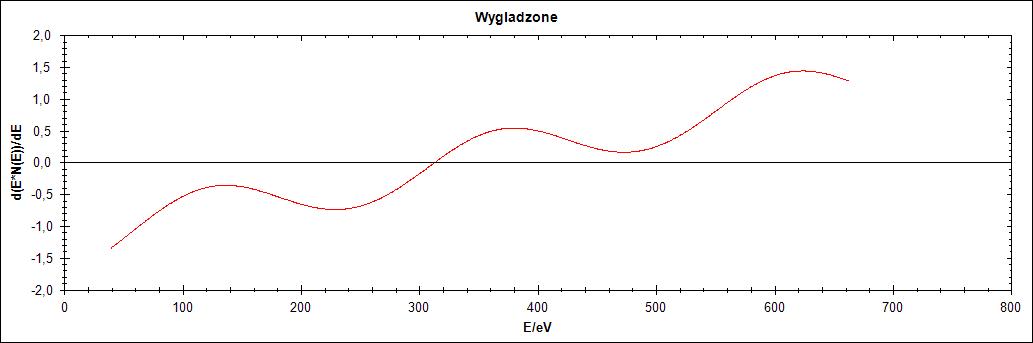
Rysunek 9. Przebieg 3) i jego warianty: zaszumiony oraz wygładzony
Na Rysunkach 10-12 widać wyniki działania algorytmu na kolejnych przebiegach z Rysunku 9 dla kolejnych wartości parametrów Δ.

Δ = 1
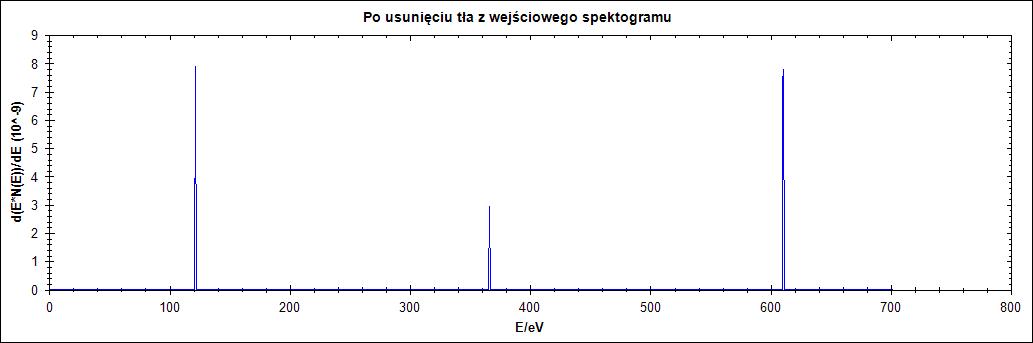
Δ = 2
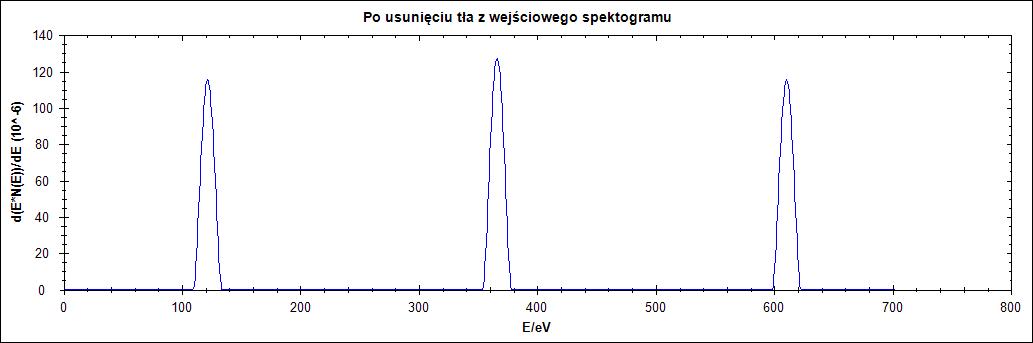
Δ = 25
Δ = 77
Rysunek 10. Działanie algorytmu dla przebiegu oryginalnego dla parametru Δ = 1,2,25,77 w kolejności od góry do dołu
Na rysunku 10. wyraźnie widać wpływ parametru delta. Dla zbyt małych jego wartości przebieg zostaje wyzerowany. Przy zwiększaniu wartości delta następuje przesunięcie przebiegu oraz zwiększenie szerokości połówkowej piku. Co ciekawe dla wartości delta równej 2 w przeciwieństwie do poprzednich przebiegów widzimy bardzo wyraźne szpilki.

Δ = 1

Δ = 2
Δ = 25
Δ = 77
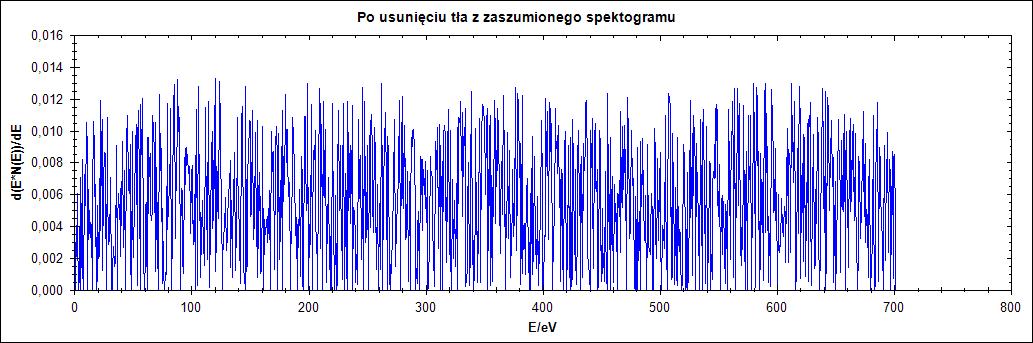
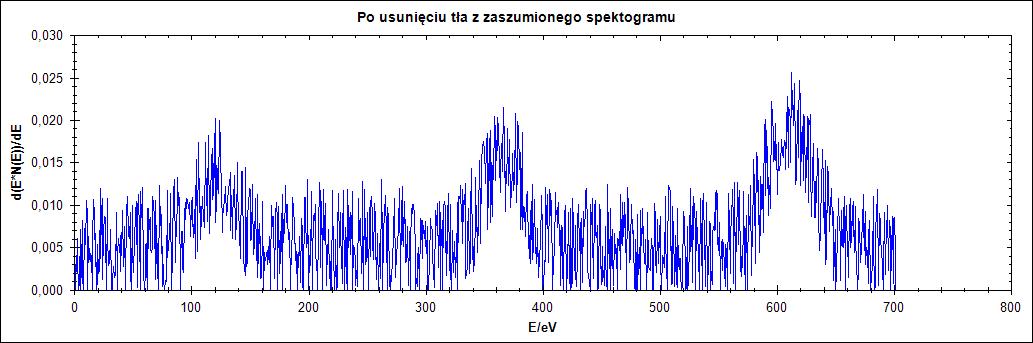
Rysunek 11. Działanie algorytmu dla przebiegu zaszumionego dla parametru Δ = 1,2,25,77 w kolejności od góry do dołu
Na rysunku 11. widać, że mocno zaszumiony przebieg wręcz uniemożliwia odczytanie pików. Dla parametru delta równego 77 istnieje jednak możliwość odczytania wartości piku.

Δ = 1
Δ = 2
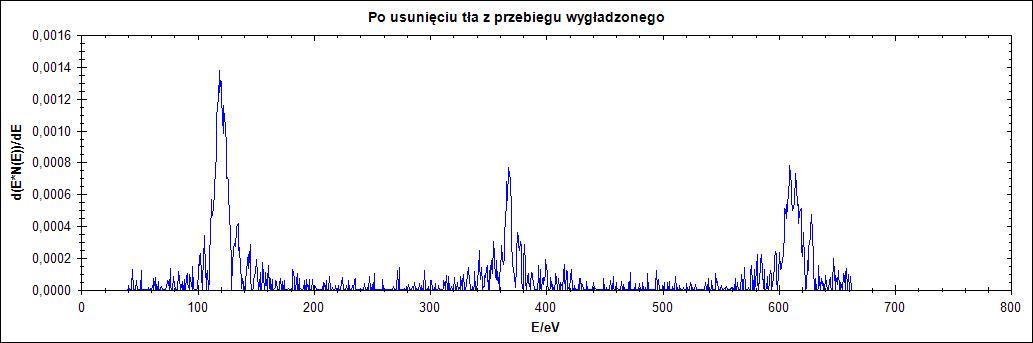
Δ = 25
Δ = 77
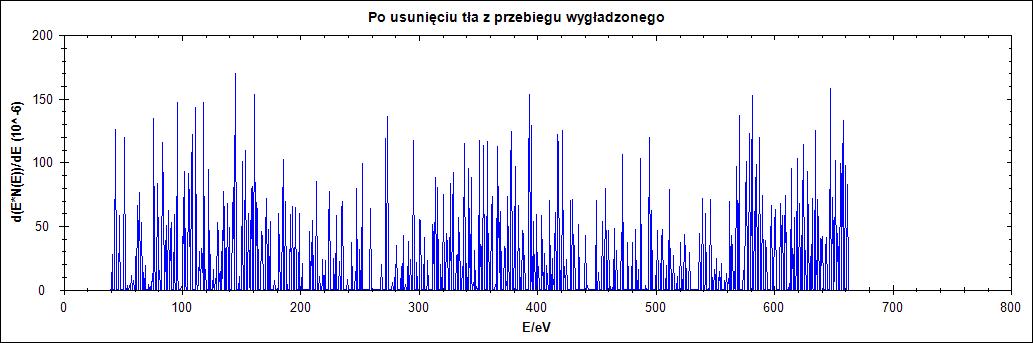
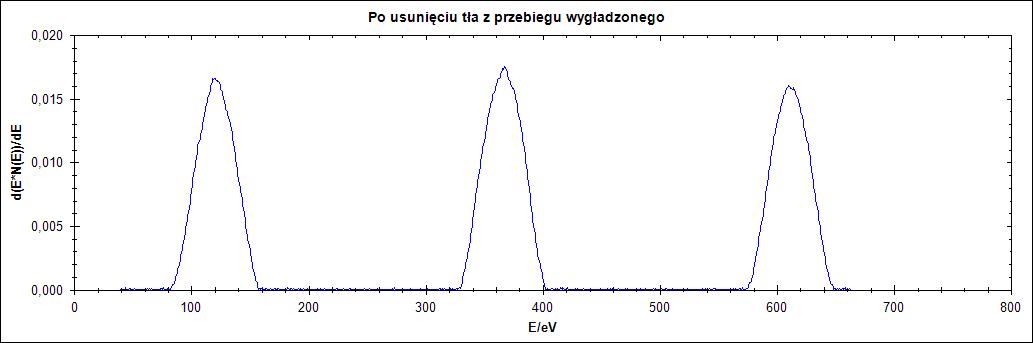
Rysunek 12. Działanie algorytmu dla przebiegu wygładzonego dla parametru Δ = 1,2,25,77 w kolejności od góry do dołu
Na rysunku 12. widzimy, że jeśli przebieg wejściowy zostanie poddany wygładzaniu algorytmem Savitzky’ego – Golay’a otrzymamy znacznie lepsze wyniki. Dla niskich wartości parametru delta nadal nie otrzymujemy nic sensownego to jednak dla wartości 25 i szczególnie 77 otrzymujemy sensownie usunięte tło.
Ostatni, czwarty przebieg również przechodzi przez oś OX. W odróżnieniu od przebiegu 3 jest malejący. Na Rysunku 13 przedstawiono trzy warianty tego przebiegu.
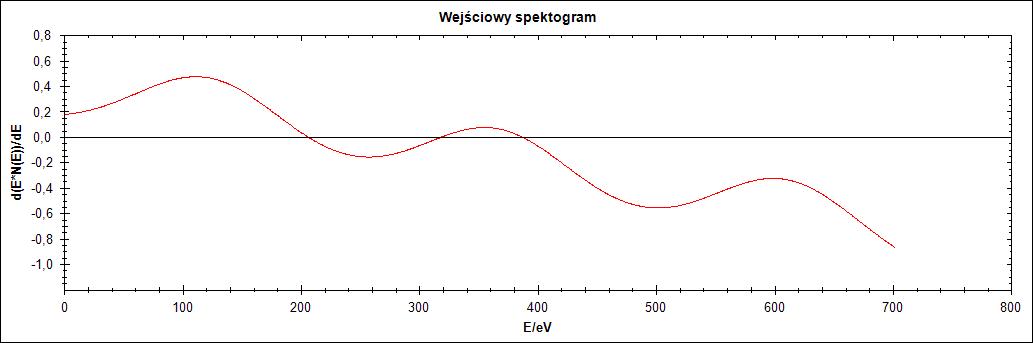
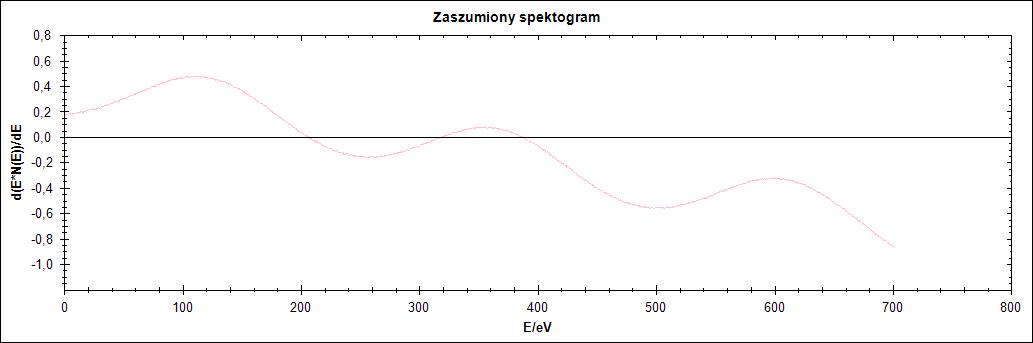
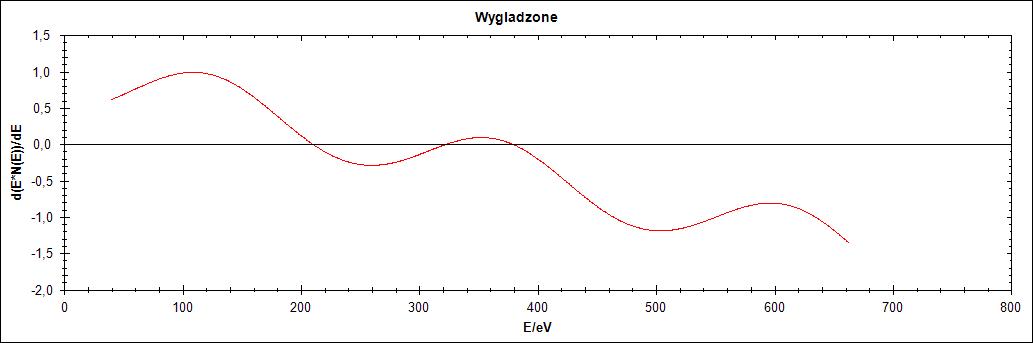
Rysunek 13.Przebieg 4) i jego warianty: zaszumiony oraz wygładzony
Na Rysunkach 14-16 widać wyniki działania algorytmu na kolejnych przebiegach z Rysunku 13 dla kolejnych wartości parametrów Δ.

Δ = 1

Δ = 2
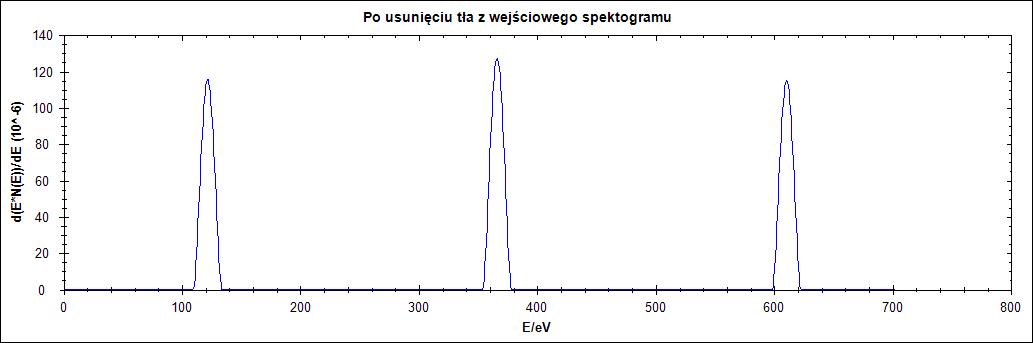
Δ = 25
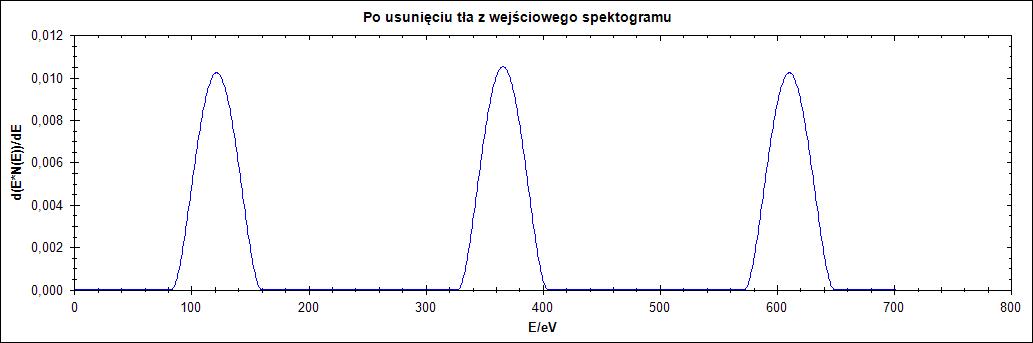
Δ = 77
Rysunek 14. Działanie algorytmu dla przebiegu oryginalnego dla parametru Δ = 1,2,25,77 w kolejności od góry do dołu
Na rysunku 14. wyraźnie widać wpływ parametru delta. Dla zbyt małych jego wartości przebieg zostaje wyzerowany. Przy zwiększaniu wartości delta następuje przesunięcie przebiegu oraz zwiększenie szerokości połówkowej piku. Co ciekawe dla wartości delta równej 2 w przeciwieństwie do poprzednich przebiegów widzimy bardzo wyraźne szpilki.

Δ = 1
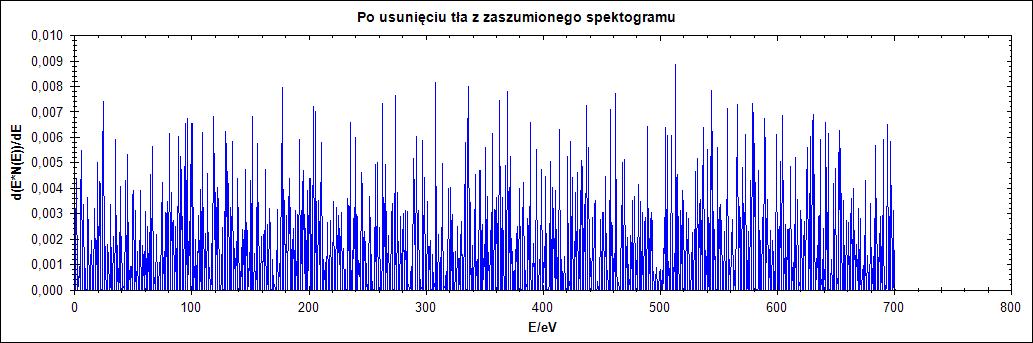
Δ = 2
Δ = 25
Δ = 77
Rysunek 15. Działanie algorytmu dla przebiegu zaszumionego dla parametru Δ = 1,2,25,77 w kolejności od góry do dołu
Na rysunku 16. widać, że mocno zaszumiony przebieg wręcz uniemożliwia odczytanie pików. Dla parametru delta równego 77 istnieje jednak możliwość odczytania wartości piku.

Δ = 1
Δ = 2
Δ = 25
Δ = 77
Rysunek 16. Działanie algorytmu dla przebiegu wygładzonego dla parametru Δ = 1,2,25,77 w kolejności od góry do dołu
Na rysunku 12. widzimy, że jeśli przebieg wejściowy zostanie poddany wygładzaniu algorytmem Savitzky’ego – Golay’a otrzymamy znacznie lepsze wyniki. Dla niskich wartości parametru delta nadal nie otrzymujemy nic sensownego to jednak dla wartości 25 i szczególnie 77 otrzymujemy sensownie usunięte tło.
Podsumowując tą część badań należy stwierdzić, że badany algorytm poprzez swoją specyficzną strukturę ma bardzo ograniczone możliwości usuwania tla z przebiegów o szerokich pikach. Jeszcze gorzej radzi sobie z przebiegami zaszumionymi. Przesuwa je oraz uwidacznia konieczność istnienia dużej intuicji badacza w doborze parametru delta. Zastosowanie wygładzania algorytmem Savitzky’ego – Golay’a znacznie polepsza pracę programu jednak nadal wymaga precyzyjnego doboru parametru delta oraz stopnia wygładzania i szerokości okna wygładzania.
Badania dla przebiegów rzeczywistych
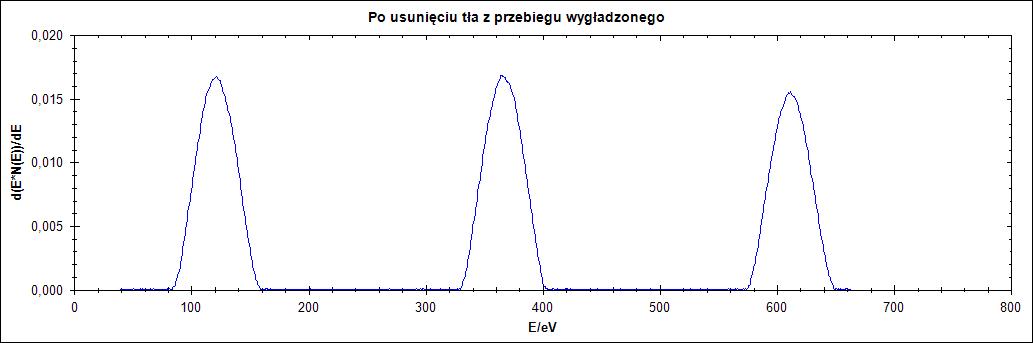
Rysunek 17. Przebieg rzeczywisty
Przebiegi wejściowe otrzymane od mojego poprzednika, który skupił się na części praktycznej badania spektroskopii elektronów Augera to pliki w formacie xml otrzymane z woltomierza Woltomierz podłączonego do karty GPIB: Hewlett-Packard 3456A.
Kolejny rysunek przedstawia efekty usuwania tła dla różnych parametrów delta.
Δ = 1
 Δ = 2
Δ = 2
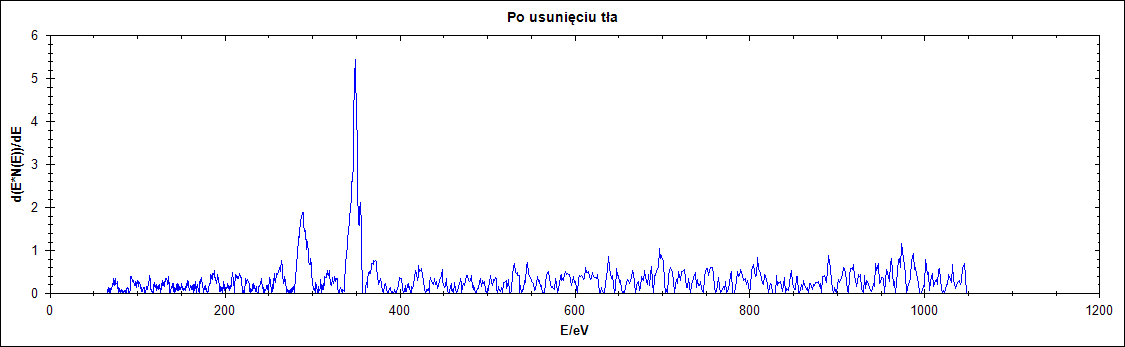
Δ = 25
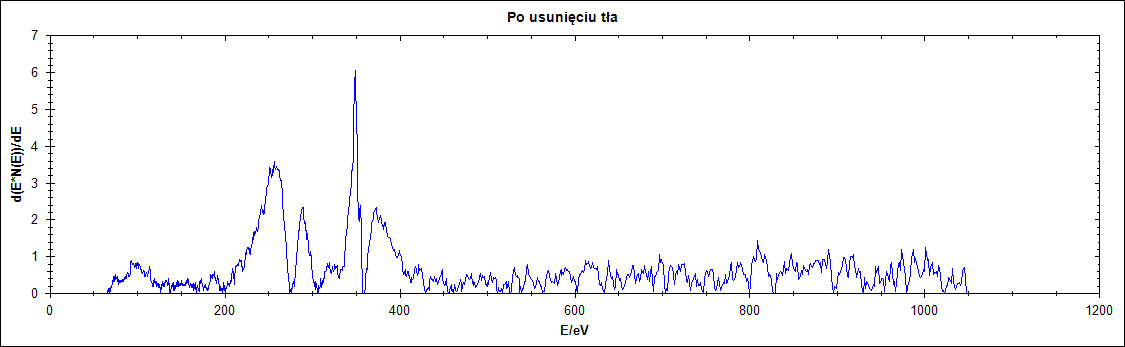
Δ =75
Rysunek 18. Usuwanie tła z przebiegu na rysunku 17 dla różnych parametrów delta.
Wyraźnie widać, że w zależności od parametru delta otrzymujemy różne przebiegi wyjściowe. Dla delty 1,2 wyniki nie niosą za sobą żadnej wartości jeśli chodzi o możliwość analizy rodzaju badanej substancji. Dla parametru 25 oraz 75 piki są wyraźnie widoczne.

Δ = 75
Rysunek 19. Wygładzanie algorytmem Savitzky’ego – Golay’a
Wygładzanie zapewnia jeszcze lepszą prezentacje wyników.
Zasymulowanie przebiegu zgodnego z badaniami twórców algorytmu
Celem potwierdzenia poprawności zrealizowanego przeze mnie programu spróbowałem skopiować przebieg zgodny z tym, jaki służył twórcom badanego przeze mnie algorytmu3.5 (w pracy twórców algorytmu rysunek 3b).
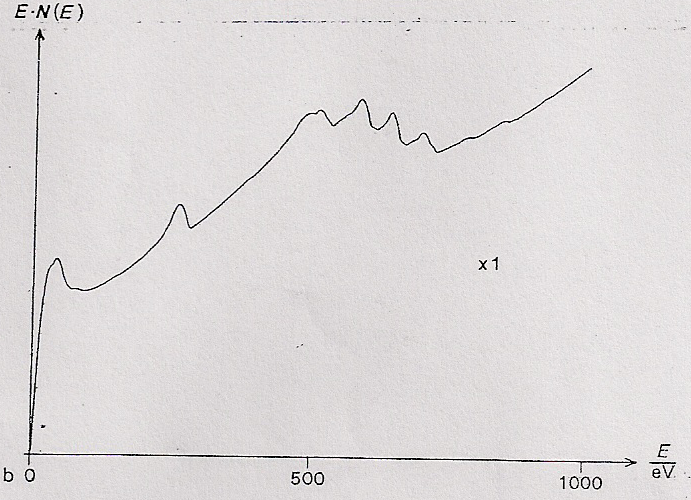
Rysunek 20. Przebieg testowy twórców algorytmu
Odwzorowanie jest niestety bardzo ograniczone, ponieważ nie dysponuję oryginalnymi przebiegami. Musiałem je stworzyć sam spisując punkty do pliku xml.
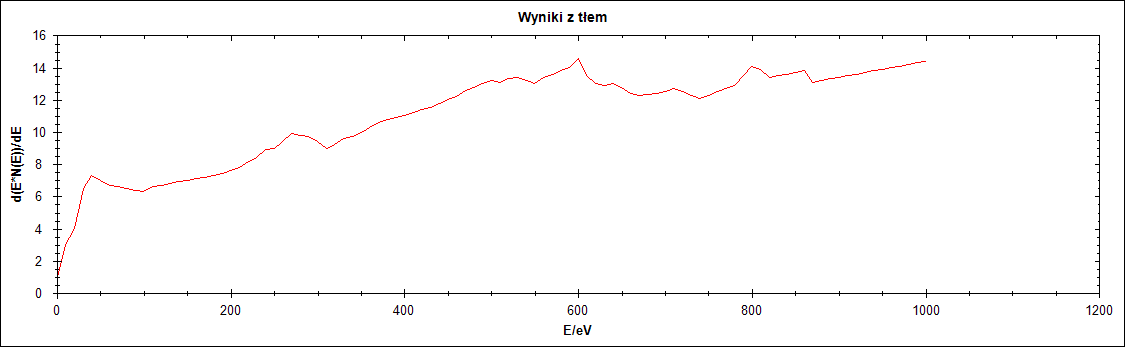
Rysunek 21. Próba odwzorowania
Stworzony przezemnie przebieg posiada niestety tylko 101 pseudo-punktów pomiarowych i w związku z tym jest „ziarnisty”. jednak w przybliżeniu oddaje rysunek 3b twórców algorytmu. W dodatku moje maksimum znalazło się przy wartości 600 eV co ma również odzwierciedlenie w przebiegu wyjściowym.
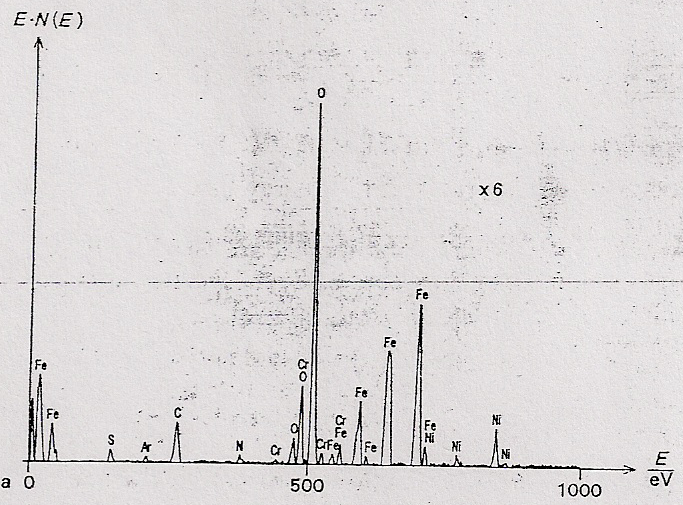
Rysunek 22. Efekt prac twórców algorytmu
Uzyskany dzięki mojemu programowi przebieg w bardzo dużym stopniu odpowiada rysunkowi 3a twórców algorytmu (w oryginalnym przebiegu twórcy algorytmu urzyli delty rownej 20 eV ja natomiast celem wiekszego wyeliminowania ‘ziarnistości’ przebiegu wejściowego zastosowałem parametr delta równy 22 eV).
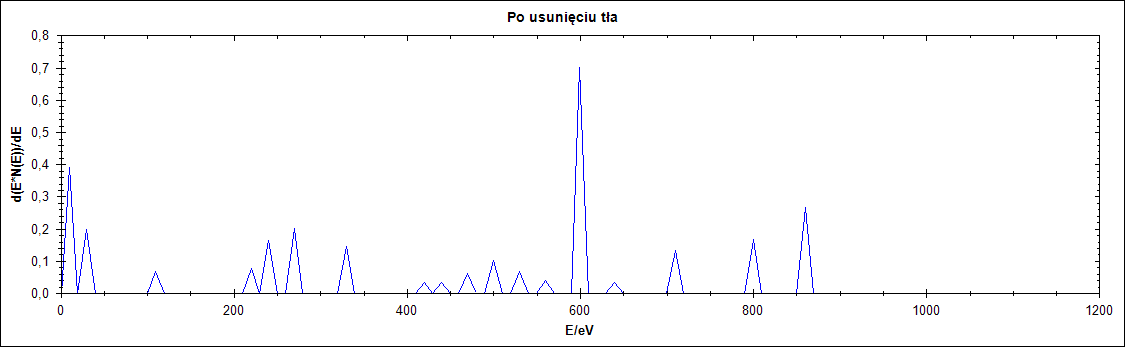
Rysunek 23. Efekt pracy mojego programu
Podsumowując część badawczą należy stwierdzić, że program komputerowy napisany przeze mnie w języku C# w pełni odzwierciedla ideę badanego algorytmu. Potwierdzają to przebiegi otrzymane celem sprawdzenia jego działania.
komentarze
Copyright © 2008-2010 EPrace oraz autorzy prac.