
ZASADA DZIAŁANIA ALGORYTMU
Algorytm został oparty o “A fast and simple method for background removal in Auger electrom spectroscopy” H.E. Bauer Instytiut fur Phisik der Universitat Hohenheim, 16 styczeń 1995
Niech 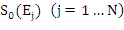 oznacza pierwotnie otrzymane spektrum lub jego część złożonego z serii niekoniecznie równomiernie rozłożonych próbek energii
oznacza pierwotnie otrzymane spektrum lub jego część złożonego z serii niekoniecznie równomiernie rozłożonych próbek energii ![]() , gdzie
, gdzie 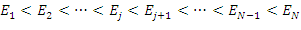 . Spektra otrzymane po kolejnych krokach algorytmu
. Spektra otrzymane po kolejnych krokach algorytmu 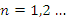 oznaczone są jako
oznaczone są jako 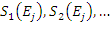
Krok 1:
Minimum spośród wartości ![]() jest odejmowane od wszystkich wartości
jest odejmowane od wszystkich wartości ![]()
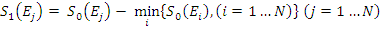
Wszystkie wartości otrzymanego zbioru ![]() są dodatnie lub równe zero, przy czym co najmniej dla jednego
są dodatnie lub równe zero, przy czym co najmniej dla jednego 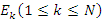 zachodzi:
zachodzi:
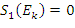
Krok 2:
Niech ![]() oznacza najmniejszą wartość próbki energii, dla której
oznacza najmniejszą wartość próbki energii, dla której 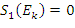 . Działanie kroku 2 zależne jest od wartości k.
. Działanie kroku 2 zależne jest od wartości k.
Jeżeli ![]() , wtedy nic nie jest zmieniane, tzn. :
, wtedy nic nie jest zmieniane, tzn. :
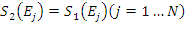
Jeżeli ![]() , wtedy:
, wtedy:
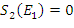
oraz
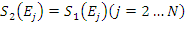
Jeżeli ![]() , wtedy:
, wtedy:
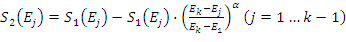
oraz
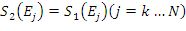 ,
,
gdzie 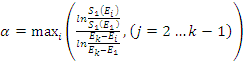
Jeżeli ![]() (co jest możliwe z powodu dyskretyzacji
(co jest możliwe z powodu dyskretyzacji ![]() co zachodzi, gdy
co zachodzi, gdy 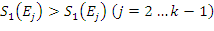 ,
, ![]() jest ustawiane na zero.
jest ustawiane na zero.
Wynikiem działania kroku 2 jest zbiór, w którym 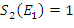 oraz
oraz 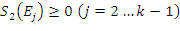 . Ta istotna właściwość jest uzyskiwana dzięki współczynnikowi
. Ta istotna właściwość jest uzyskiwana dzięki współczynnikowi 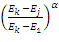
Krok 3:
Powtarza działania kroku 2, dla największych wartości próbek energii.
Niech ![]() oznacza próbkę energii o największej wartości, dla której
oznacza próbkę energii o największej wartości, dla której 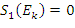 .
.
Działanie kroku 3 zależne jest od wartości k.
Jeżeli ![]() , wtedy nic nie jest zmieniane, tzn. :
, wtedy nic nie jest zmieniane, tzn. :
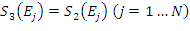
Jeżeli 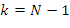 , wtedy:
, wtedy:
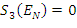
oraz
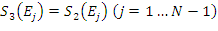
Jeżeli 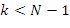 ,wtedy:
,wtedy:
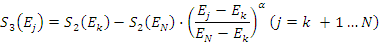
oraz
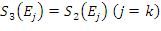 ,
,
gdzie 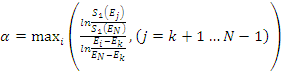
Ponownie, gdy ![]() ,
, ![]() jest ustawiane na zero. Wynikiem działania kroku 3 jest zbiór, w którym
jest ustawiane na zero. Wynikiem działania kroku 3 jest zbiór, w którym 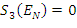 oraz
oraz 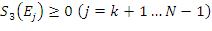 .
.
Po kroku 2 i 3, wszystkie wartości zbioru ![]() są dodatnie lub równe zero. Pierwszy i ostatni element tego zbioru jest równy zero:
są dodatnie lub równe zero. Pierwszy i ostatni element tego zbioru jest równy zero:
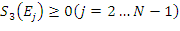
oraz
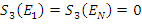 .
.
Następne kroki są procedurą usuwania tła. Jednakże przed przystąpieniem do nich należy zdefiniować parametr Δ oraz funkcję usuwającą tło. Δ, tj. limit energii określa ile tła jest usuwane. Im mniejsza wartość Δ, więcej tła jest usunięte. Funkcja usuwająca tło powinna przyjmować trzy argumenty i osiągać jedno maksimum. Dla uproszczenia przyjęta została funkcja kwadratowa.
Krok n (n = 4, 5....):
Niech ![]() i
i ![]() będą dwoma najmniejszymi wartościami próbek energii, dla których:
będą dwoma najmniejszymi wartościami próbek energii, dla których:
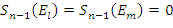
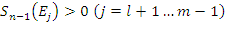
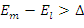
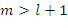
Zbiór ![]() jest wyznaczany z zależności:
jest wyznaczany z zależności:
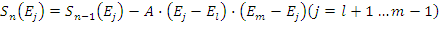
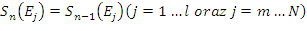 ,
,
gdzie 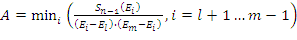
Budowa funkcji odejmującej zapewnia, że wszystkie wartości ![]() są dodatnie lub równe zero.
są dodatnie lub równe zero.
Krok n jest powtarzany dopóki nie można znaleźć ![]() i
i ![]() spełniających podanych warunków. Oznacza to zakończenie algorytmu i usunięcie tła z wejściowego spektrum.
spełniających podanych warunków. Oznacza to zakończenie algorytmu i usunięcie tła z wejściowego spektrum.
komentarze
Copyright © 2008-2010 EPrace oraz autorzy prac.